The Newton Law of
Universal Gravitation
Introduction
The only way to get the Newton Law of Universal Gravitation is to start with EFE using a spherical static symmetry and weak field approximation. Here we show that the Newton Law can be easily obtained replacing mass by closed volume. This approach is much more simple than the traditional method using a reduction of tensors from EFE.
Background: the Bulk Modulus
The bulk modulus Kb of a substance measures the substance's resistance to uniform compression. It is defined as the pressure increase needed to cause a given relative decrease in volume.
![]()
Starting with the Fluid Mechanics from 1850's, Einstein demonstrated in 1910's that spacetime:
- Can be identified to a fluid,
- Returns to its rest shape after applied a stress (elasticity properties).
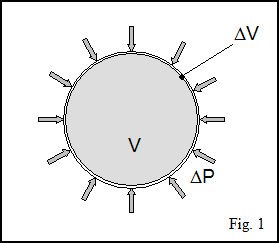
Therefore, the Bulk Modulus equation (1) can be applied to spacetime. It means that the displacement of spacetime made by a closed volume exerts a pressure on the surface of the volume, which conducts to a volume decrease, as shown in fig. 1.
Background: Elasticity law
Elasticity phenomena follows the well-known logarithmic law:
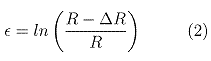
The Schwarzschild Metric gives an order of magnitude of the curvature of spacetime. This latter is infinitesimal. For example, the ratio curvature of spacetime/radius, or DR/R, is 1.4166 x 10-39 for the proton, with M = 1.672 E-27, R = 8.768 E-16, G = 6.674 E-11, cē = 8.987 E+16, and DR/R = GM/Rcē. The formula DR/R is the first order approximation of the square root of the r radius coefficient in the Schwarzschild Metric. Please see our Schwarzschild Metric web page for further information.
Under that conditions, whatever the formulae used, logarithmic or not, the curvature of spacetime can be considered as a linear function since we are working on an infinitesimal segment near to the point zero. So, this formulae becomes:
![]()
or, with volumes:
![]()
For the moment, coefficients of elasticity of spacetime eR and eV are unknown.
Curvature of spacetime Dx
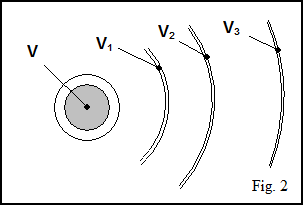
A closed volume V inserted into a flat spacetime pushes spacetime to make room (fig. 2). So, the following volumes are identical:
![]()
Since the spacetime curvature is infinitesimal, the coefficient of elasticity of spacetime e v is constant, as any coefficient of elasticity if we are working in a very small segment near zero. So, combining (4) and (5) gives:
![]()
Curvature vs displacement of spacetime
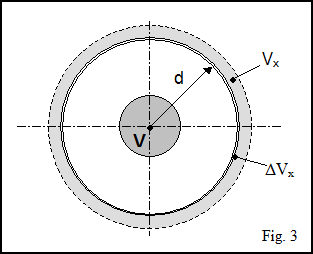
There should not be any confusion between a simple displacement of spacetime, Vx, produced by the insertion of a closed volume into a flat spacetime, and the curvature DVx= evVx due to the elasticity of spacetime (fig. 3).
Solving Dx = f(DR)
Since the DV's are infinitesimal, the volume DVx is the product of Dx by the surface Sx (fig. 4):
![]()
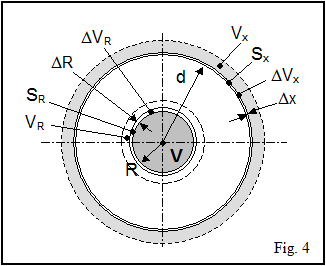
On the same manner, the volume DVR is the product of DR by the surface SR:
![]()
From (6) we have:
![]()
Combining equations (7), (8) and (9) gives:
![]()
Finally, we get:
![]()
where:
- R is the radius of the closed volume VR producing the spacetime displacement,
- DR is the curvature of spacetime on the surface of the closed volume VR,
- d is the distance of the point of measurement,
- Dx is the curvature of spacetime at distance d.
Curvature (Dx) vs. Mass (M)
As seen in figure 5, a relation exists between the curvature of spacetime, DR (or Dx at a distance "d" from R), and the mass of the object, more precisely its "mass effect":
![]()
This formulae isn't original since it comes from Einstein : Mass is identified to spacetime curvature
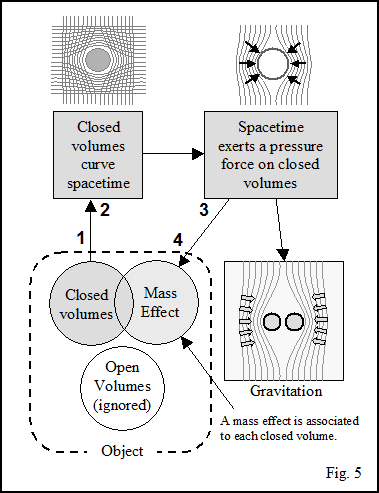
It is the pressure of the spacetime curvature on the closed volume that produces the mass effect. This suggests that the latter is inversely proportional to the surface S, or [1/L2]. The mass effect is also proportional to the volume, or [L3]. Therefore, the dimensional quantity of the mass effect is [1/L2][L3] = [L]. So, the latter can be written as : [M] ≡ [L].
This deduction is in accordance with EFE and their solutions as the Schwarzschild Metric that gives identical results. At this point, we do not know the relation between DR and M but, in referring to Einstein's works, we have good reasons to believe that this relation is a simple linear function like:
![]()
where K is an constant having the dimensional quantity of [L/M], as we have seen.
The challenge, now, is to calculate K to get the Newton's law of Universal Gravitation.
The Newton Law
Porting equation (13) in (11) gives:
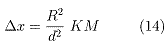
or:
![]()
Since x = ct, replacing R2 by c2t2 gives:
![]()
or:
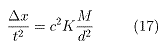
The value Dx/t2 has the dimensional quantity of an acceleration [L/T2]. So, replacing this fraction by the acceleration symbol "a", we get:
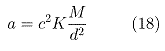
On the other hand, the multiplication of a constant c2 by a second constant K gives another constant. So, we can replace the product c2K by a new unknown constant, G for example:
![]()
or: (this equation isn't necessary here but will be used for the calculation of the Schwarzschild Metric)
![]()
Porting (19) in (18) gives:
![]()
This new constant G = c2K have the dimensional quantity :
- c2 : Dimensional quantity = [L2/T2]
- K : Dimensional quantity = [L/M],
So, the dimensional quantity of this new unknown constant G is c2K = [L2/T2][L/M] = [L3/MT2].
On the other hand, we know that the force is the product of an acceleration by a mass. Therefore, equation (21) can be written as follow:
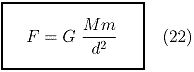
About G we remark:
- G is a constant since it is the product of two constants, c2 and K,
- Its dimensional quantity is [L3/MT2].
So, we can identify G to the constant of gravitation issued from experimentation: G = 6,67428.10-11. In other words,
Equation (22) can be identified to the
Newton Law of Universal Gravitation