Introduction

Increase of mass of relativistic particles is part of special relativity. However, this phenomenon remains particularly obscure. To date, no one can explain, with simple words and without the aid of mathematics, this enigma.

The new theory described in the main page of this website allows us to have a simple and rational explanation of this strange phenomenon.

Length contraction

Relativity says that, under relativistic speeds, time expands and lengths contract. A simple demonstration is given in 1923 by Einstein himself in his book "The theory of special and general relativities".

Length contraction is defined by the following formula

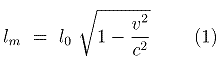
with

• l_m = Measured length
• l₀ = Proper length
• v = Speed of object
• c = Speed of light

Mass increase

Lets consider a particle at rest (fig. a). Its closed volume will produce a curvature of the spacetime. Geodesics are spaced of l₀.

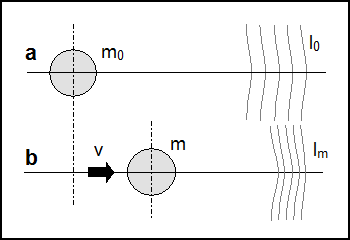
If this particle moves at relativistic speed v, spacetime geodesics seems to shrink. This is the well-known phenomenon of length contraction mentioned in the previous paragraph (see note 1).

More the geodesics are close to each other, more dense the spacetime curvature will be. In other words, the spacetime curvature is inversely proportional to the space between two geodesics (see note 2).

So, relation (1) becomes:

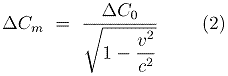
with

• ΔC_m = Differential element of measured spacetime curvature
• ΔC₀ = Differential element of proper spacetime curvature
• v = Speed of particle
• c = Speed of light

Since the curvature is function of mass (see note 3), we can replace the spacetime curvature C by the mass m, which gives us the expression of the measured mass "m" vs the proper mass "m ₀" (see note 4).

 
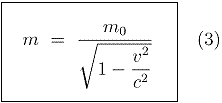
This new theory gives a very simple and rational
explanation of the mass increase of relativistic particles
 

Note 1: The phenomena of special relativity (length contraction, time and mass dilation) are real since we can make measurements. However, the special relativity principles indicate that an absolute reference does not exist. For example, if we have two rules A and B moving one relative to the other, the rule B will see the rule A contracted and reciprocally. It is obvious that the rule A can't be smaller AND larger than the rule B. It means that special relativity formulae are related to measured values. Thus, if we measure 5 times the rule A from B at different relativistic speeds, we will get 5 different lengths. However, there is a privileged length which is the length measured on the object itself. This measure is called "proper value". In this paper, proper values are denoted with a 0 index.
Note 2: The spacetime curvature is the difference of displacement ΔR of a geodesic vs to the same geodesic in a Minkowski space. The Schwarzschild metric gives an order of magnitude of this spacetime curvature: 1.4166 E-39 for the proton on its surface. This value is much smaller at distance r. Thus, regardless of the function used, the portion of the curve on which we work is linear. Taking into account this linearity, there is no objection to consider that the curvature is inversely proportional to the space between two geodesics.
Note 3: The relationship between curvature and mass is calculated on our web page "Calculation of the mass effect" in the "Mathematical demonstration" section. Its expression is ΔR = KM. However, the nature of this formula does not matter because it is out of the subject of this paper. This website covers the calculation of the coefficient to be applied to a proper value to get the measured value. This coefficient is called γ (or 1 / γ) in scientific literature. It means that the relationship between the spacetime curvature and mass aren't affected by this study. For example, if we make 5 measurements of the curvature of spacetime at different speeds, we will not have 5 different relationships between ΔR₀ (ΔR proper) and M, but only one, applicable in all cases. ...but we will have 5 different coefficients γ.
Note 4: The principles of special relativity state that the mass of a relativistic particle increases, but the converse is also true if we swap the reference systems. If we could pick up a measuring device on a particle in movement, this device would indicate that our spacetime, in which we live, is much more dense as we see it. Thus, a section of the LHC for example, with a mass of 3 tons, measured from a device located on the particle in motion, would have a mass of 3000 tons if γ = 1000. From our view, the mass of a relativistic particle increases, but from the particle's view, it is our world that increases. In all cases, the proper mass of the particle or that of our world remains unchanged.

Close the window