The Schwarzschild Metric
Introduction
Here we show that the Schwarzschild Metric can be easily obtained starting from closed volumes instead of the mass concept. This demonstration does not require complex tensor manipulations as in the traditional method.
The Minkowski Metric
The expression of the Minkowski Metric, in spherical coordinates, is:
![]()
The Schwarzschild Metric refers to a static object with a spherical symmetry. It is built from a Minkowski Metric, in spherical coordinates, with two unknown functions: A(r) and B(r) :
![]()
Remembering that the Minkowski Equation follows the Lorentz Invariance, the only way to get this invariance is to set A(r) = 1/B(r).
From a mathematical point of view, we get the same result developing and simplifying EFE with correct parameters. Details of calculations are described in many articles and books concerning General Relativity. This conducts to the following equality:
![]()
Notes: Some authors prefer writing A(r)B(r) = K with K=c2. In that case, the term c2 must be excluded from the Minkowski Metric, equation 1. However, in both cases, result is identical. On the other hand, in order to simplify equations, some Authors also replace c and G by 1. To avoid inconsistent expressions, we do not follow this rule in this webpage because a simple number, "1" in this case, does not have a dimensional quantity like c2 or G, [L2/T2] or [L3/MT2] respectively.
The Schwarzschild Metric
To calculate the Schwarzschild Metric, we can start with the figure of the main text concerning a convex curvature of spacetime (fig. 1):
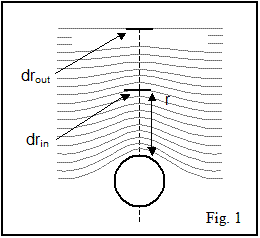
where :
- drout is an elementary differential radial variation outside of any mass,
- drin is an elementary differential radial variation inside a Schwarzschild space,
- r is the point of measurement.
As in the Newton Law webpage, we have:
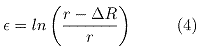
where:
- e is a coefficient of the increase of spacetime curvature at distance r,
- DR is the initial curvature of spacetime produced by the closed volume,
The order of magnitude of e being 10E-39, we can use the first order approximation:
![]()
Since e is a simple coefficient, we can calculate the relation between two differential elementary radius drout and drin, out and in a gravitational field:
![]()
Since e << 1, the equivalent formula is:
![]()
or, elevating in square:
![]()
Developing the denominator (1 – e)2 = 1 - 2e + e2 and ignoring the last term e2, we obtain:
![]()
This result is nothing but the radial component of the Schwarzschild Metric, that is to say the function A(r) of dr2 in equation 2. The calculation of B(r) is immediate, taking into account that A(r) B(r) = 1 from equation 3:
![]()
![]()
So, equation 2 becomes:
![]()
In the Newton Law webpage, we have obtained the following result: DR = KM (equ. 13), where K = G/c2 (equ. 20). So, equation 5 can be rewritten as:
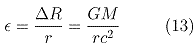
Finally, porting this expression in equation 12 gives:
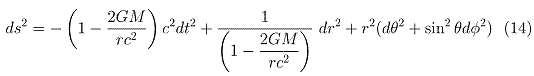
As we see,
The proposed theory, based on closed
volumes, gives an easy and consistent
explanation of the Schwarzschild Metric.